Mesh Mess

FEM, CFD, CAE, and all that.

Tag: time integration

10/22/2009

A sample of toy FDM code

Solving equation

u_t-u''=f(x,u)

f(x,u)=-2+2*(\sin(u)-\sin(x^2))

Time integration is full implicit, and during each time step Newton’s method is employed.

PROGRAM MAIN
!--------------------------------------------------
!Implicit time evolution of equation
!u_t-u''=f(x,u)
!f(x,u)=-2+r*(sin(u)-sin(x^2)),r=2
!--------------------------------------------------
! t=time points
! dt=time step
! h=neighboring nodes distance
! u=unknown
! x=node location
! n=No. of unknowns

!USE SUNPERF

IMPLICIT NONE
INTEGER(4) :: n
REAL(4) :: elapse,time(2),etime
REAL(8) :: t=0,dt=0.1
REAL(8) :: h
REAL(8),ALLOCATABLE :: u(:),x(:)
INTEGER(4) :: count,i

n=50
h=1/(DBLE(n)+1.)
ALLOCATE (x(n),u(n))
x=(/(i*h,i=1,n)/)
u=(/((i*h)**0.5,i=1,n)/)

OPEN(UNIT=100,FILE='data',STATUS='UNKNOWN',ACTION='&
     &WRITE')
DO i=1,n
   WRITE(100,*) t,x(i),u(i)
END DO

DO WHILE (t<1.0)    
CALL newton(n,h,dt,u,x)    
t=t+dt    
DO i=1,n       
WRITE(100,*) t,x(i),u(i)    
END DO END DO CLOSE(UNIT=100) 
elapse=etime(time) 
WRITE(*,*) 'elapsed:',elapse 
END PROGRAM MAIN 
!-------------------------------------------------- 
SUBROUTINE newton(n,h,dt,u,x)   
IMPLICIT NONE   
INTEGER(4),INTENT(IN) :: n   
REAL(8),INTENT(IN) :: x(n),h,dt   
REAL(8),INTENT(INOUT) :: u(n)   
REAL(8) :: r=2,c(n),error,b(n,1),b0(n,1),a(2,n)   
REAL(8) :: alpha=1.0,beta=-1.0   
INTEGER(4) :: info,i,iter   
c=u*h*h/dt   
iter=0   
error=1   
DO WHILE (error>1.e-13)
     iter=iter+1
     a(1,:)=-1
     a(2,:)=2+h*h/dt
     b(:,1)=(-2+r*(SIN(u)-SIN(x*x)))*h*h+c
     b(n,1)=b(n,1)+1
     CALL DSBMV('u',n,1,alpha,a,2,u,1,beta,b,1)
     b=-b
     a(2,:)=a(2,:)-r*COS(u)*h*h
     CALL DGTSV(n,1,a(1,2:),a(2,:),a(1,2:),b,n,info)
     error=MAXVAL(ABS(b))
     u=u+b(:,1)
  END DO
  WRITE(*,*) 'INFO',info,'Number of iterations:',iter
END SUBROUTINE newton
!--------------------------------------------------

Output would be like:

% f95 -dalign implicit_newton.f95 -xlic_lib=sunperf
% a.out
 INFO 0 Number of iterations: 4
 INFO 0 Number of iterations: 4
 INFO 0 Number of iterations: 4
 INFO 0 Number of iterations: 4
 INFO 0 Number of iterations: 4
 INFO 0 Number of iterations: 3
 INFO 0 Number of iterations: 3
 INFO 0 Number of iterations: 3
 INFO 0 Number of iterations: 3
 INFO 0 Number of iterations: 3
 elapsed: 0.061407

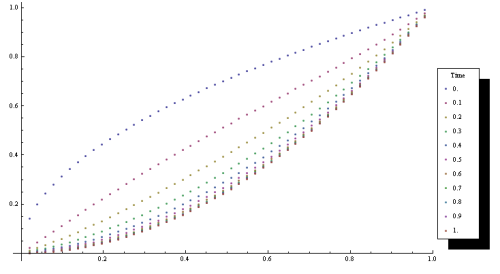
Of course the exact solution is u(x)=x^2. Here is time evolution plot of the numerical solution.

implicit_newton

1 Comment
07/15/2009

Mixed-Eularian-Lagrangian method

In last post I talked wrote about a time integration for NS equation. As a special case, time update for potential flow is actually easier, due to fact that

1. the governing equation, i.e. the Laplace equation is linear.

2. the solution dependes only on the boundary condition, in which only the free surface boundary condition is the tricky part.

3. Even though the field equation is in Eularian representation, the free surface can be described using Lagrangian representation.

For free surface potential flow, the time updating of the problem is twofold: update the (free surface) geometry and update the boundary conditioin at the free surface. Without mentioning the boundary condition at other part of the domain boundary, we are solving the problem characterized by

Field equation: \nabla^2 \phi=0,\quad \forall x\in \sigma

Free surface kinetic boundary condition(FSKBC): D\vec{r}/Dt=\nabla \phi, \quad \forall x\in \gamma_0

Free surface dynamic boundary condition(FSDBC): \phi_t+1/2 (\nabla\phi)^2+gz+p/\rho=0,\quad \forall x\in \gamma_0

The first boundary condition says that the particle velocity for material particle on the free surface, i.e. the velocity of free surface, equals to the flow velocity defined by velocity potential. The second boundary condition is the  Bernoulli equation, with constant on RHS assigned to 0, which could be looked as consumed by \phi_t. Remembering that

\phi_t=D\phi/Dt-\vec{u}\cdot \nabla \phi=D\phi/Dt-(\nabla \phi)^2

FSDBC can be converted to

D\phi/Dt=1/2(\nabla \phi)^2-g\eta-p/\rho,\quad \forall x\in \gamma_0

The plan of mixed-Eularian-Lagrangian(MEL) method, is to solve \phi^n at time t_n, then use the BC equations to update the boundary condition. One should remember, the LHS of BC equations use material particle as variable, i.e. in Lagrangian representation. Denote particle on the free surface by \zeta, MEL is characterized by two steps:

1. Solve field equation with BCs with variable at t_n, i.e. \phi^n, \vec{r}^n;

2. Update the BCs at the free surface using

(\vec{r}^{n+1}(\zeta)-\vec{r}^n(\zeta))/\Delta t=\nabla \phi^n(\zeta)

(\phi^{n+1}(\zeta)-\phi^n(\zeta))/\Delta t=1/2(\nabla \phi^n(\zeta))^2-g\eta-p/\rho

As mentioned at the end of last post, usually the computing cost is characterized by the first step, while the second step concerns the stability and convergence.

Leave a comment
07/14/2009

Time integration again

In the post time integration: incompressible flow I explained a scheme example using PFEM. I don’t think it’s really “meshless”, even though by definition of same group it is. Personally, I more tend to see it a FEM with time-updated elements and shape functions, at lease mathematically. Anyway, the nice way of time spitting is what interests me here. Within an iteration, the variables are found following:

\cdots\longrightarrow u_i^n, p^n\longrightarrow u_i^{\ast}\longrightarrow p^{n+1}\longrightarrow u_i^{n+1}\longrightarrow\cdots

For each step above, equation for the unknowns to be solved are: Elliptic equation for u^{\ast}, elliptic equation for p^{n+1} and algebra/finite difference for u_i^{n+1}. This means for this particular time updating plan, a single linear elliptic equation solver can be used. Remember, this virtue is due to two things, the first is the MEL to eliminate the annoying nonlinear convection term, second, the time splitting using u^{\ast} as the intermediate variable. In summary, this scheme, as many other ones, gains the sequential solution by paying the price with solving one more variable (implicitly). It can be seen that within one iteration the solving of field equation costs most of the computing, while the choice of time integration scheme is the main source of stability issues.

1 Comment
06/28/2009

Time integration: incompressible flow

I try to consolidate last post using a scheme for incompressible flow under Lagrangian description. Those two condition make somehow make the plan much easier against general case. Since for the moment I am reading this paper, I will take some of its ideas, even though this whole modern time splitting scheme by projection methods owns its origin to Chorin and Temam in 1960’s.

Consider the governing equations:

\frac{D\rho}{Dt}=-\rho\frac{\partial u_i}{\partial x_i}  (MEL-in mixed-Eulerian-Lagrangian form) or \frac{\partial u_i}{\partial x_i}=0 (Eulerian form)

\frac{Du_i}{Dt}=-\frac{1}{\rho}\frac{\partial p}{\partial x_i}+\mu\frac{1}{\rho}\frac{\partial^2 u_i}{\partial x_j\partial x_j}+f_i

For a specific material particle \xi, both the displacement and velocity are functions of time:

u=u(\xi,t)\quad x=x(\xi,t)

Now, let’s suppose the variables at time t_i are known as \phi^n=\phi(\xi,t_n). For velocity we have the general time integration:

\frac{u_i^{n+1}-u_i^n}{\Delta t}=(1-\theta)(-\frac{1}{\rho^n}\frac{\partial p^n}{\partial x_i^n}+\mu\frac{1}{\rho^n}\frac{\partial^2 u_i^n}{\partial x_j^n\partial x_j^n}+f_i^n)

+\theta(-\frac{1}{\rho^{n+1}}\frac{\partial p^{n+1}}{\partial x_i^{n+1}}+\mu\frac{1}{\rho^{n+1}}\frac{\partial^2 u_i^{n+1}}{\partial x_j^{n+1}\partial x_j^{n+1}}+f_i^{n+1})

In equation above, partial derivative by x_i^{n+1} means take the derivative within the spatial configuration of time t_{n+1}. This spatial domain is obtained using velocity updating:

x(t_{n+1})=x(t_n)+u(t_n)\Delta t

Parameter \theta varies between 0 and 1. When \theta=0, RHS is based on time t_{n+1}, i.e. implicit scheme, while when \theta=0 we have explicit scheme. Generally, implicit schemes are prefered for its stability merit, which I adopt in this post. So we have

\frac{u_i^{n+1}-u_i^n}{\Delta t}=-\frac{1}{\rho^{n+1}}\frac{\partial p^{n+1}}{\partial x_i^{n+1}}+\mu\frac{1}{\rho^{n+1}}\frac{\partial^2 u_i^{n+1}}{\partial x_j^{n+1}\partial x_j^{n+1}}+f_i^{n+1}

There are two choices to implement the discrete governing equations. One is two resolve u^{n+1}_1,u^{n+1}_2,u^{n+1}_3,p^{n+1} all together, by coupling equation above with mass conservation equation of Eulerian form \nabla\cdot \vec{u}=0. The other one is try to update velocity separately, for this purpose we have to transform the mass equation, because it is this equation that couples velocities in different directions. On the other hand, we also want to decouple the pressure and velocity. Before introduce the scheme, let’s first take a look at the physical interpretation of the coordnate system.

When solving the dynamical problem numerically, we hope at one time step, we take care of time derivatives and space derivatives separately. Suppose I am examining a fixed time step t_n\rightarrow t_{n+1}, the material particle indexed by \xi can actually be indexed by the spatial position (in Eulerian coordinates) \vec{x}. In other words, when we talk about some specific material particle, it can be labeled with location \vec{x} at time t_n. So x^{n+1}(\xi)=x^{n+1}(x) simply means the t_{n+1} location of some particle which at t_n occupies x . By this notation, the momentum equation, assuming constant density and body force, is

\frac{u_i^{n+1}(x^{n+1})-u_i^n(x)}{\Delta t}=-\frac{1}{\rho}\frac{\partial p^{n+1}}{\partial x_i^{n+1}}+\mu\frac{1}{\rho}\frac{\partial^2 u_i^{n+1}}{\partial x_j^{n+1}\partial x_j^{n+1}}+f_i

and the mass equation is

\frac{\rho^{n+1}(x^{n+1})-\rho^{n}(x)}{\Delta t}=-\rho\frac{\partial u_i}{x_i}

In order to decouple velocity and pressure in momentum equation, we split it:

\frac{u_i^{n+1}(x^{n+1})-u^{\ast}(x)}{\Delta t}+\frac{u^{\ast}(x)-u_i^n(x)}{\Delta t}=[-\frac{1}{\rho}\frac{\partial (p^{n+1}-p^n)}{\partial x_i}]+[-\frac{1}{\rho}\frac{\partial p^n}{\partial x_i}+\mu\frac{1}{\rho}\frac{\partial^2 u_i^{\ast}}{\partial x_j\partial x_j}+f_i]

The two terms on both side form pairs accordingly. The second terms gives an implicit scheme for intermediat variable u^{\ast}. Similar split in mass equation gives

\frac{\rho}{\Delta t}\frac{\partial u^{\ast}_i}{\partial x_i}=\frac{\partial^2 p^{n+1}}{\partial x_i^2}

which gives p^{n+1}, then the first terms in split momentum equation is used to obtain u^{n+1}_i:

u^{n+1}_i=u^{\ast}_i-\frac{\Delta t}{\rho}\frac{\partial (p^{n+1}-p^n)}{\partial x_i}

The three equations above, are to be used to find u^{\ast},p^{n+1},u^{n+1} sequentially. This means to solve two spatial domain PDEs for the first two equations, and take one derivative for the last.

2 Comments
06/27/2009

Time integration in a dynamical FEM prob.

For any dynamical problems involving spatial evolution, each step is to be solved by proposed spatial discretization scheme. But unlike steady/static problem, which requires no particular time updating, dynamical problem requires discretization in one more dimension, the time.

This leads to one of the most important and, to me,  most messy part of numerical simulation. Say,  at any time t_1, spatial problem is (to skip the boundary condition)

\mathcal{L}\phi(x,t_1)=0

with time evolusion equation

\frac{Du(x,t)}{Dt}=\mathcal{F}u(x,t)

in which both \mathcal{L} and \mathcal{F} are global operators in the spatial domain. At each time like t_1, the first equation is to be solved, in discretized version, one or another. And the second equation is used to formulate the spatial domain in next step, after the local velocity u is resolved and used to update the spatial configuration using

x(t_2)=x(t_1)+u\Delta t

Here comes the tricky part. In equation above, which time to use for velocity? In particular, should one use u(x(t_1),t_1) or u(x(t_2),t_2)? And to the next step, when one tries to solve (this is so called “time integration”, because it’s discrete version of taking integral) differential equation of u, what time should be introduced on RHS?

There are various time updating plans in use, which can be catogorized into implicit and explicit families, depending on whether the unresolved variable at next time step show up on RHS. And the story continues in balancing the advantage/disadvatange of those catogories.

Leave a comment